Chapter 1 Test Review What Is the Value of the Expression (-8)^4
2.iii: Evaluate, Simplify, and Translate Expressions (Part 1)
- Page ID
- 4978
Skills to Develop
- Evaluate algebraic expressions
- Identify terms, coefficients, and like terms
- Simplify expressions by combining like terms
- Translate word phrases to algebraic expressions
Be prepared!
Before you go started, accept this readiness quiz.
- Is \(n ÷ 5\) an expression or an equation? If you missed this problem, review Instance 2.1.4.
- Simplify \(four^v\). If you lot missed this problem, review Example ii.ane.6.
- Simplify \(1 + 8 • nine\). If you lot missed this problem, review Instance 2.i.eight.
Evaluate Algebraic Expressions
In the last section, we simplified expressions using the society of operations. In this section, we'll evaluate expressions—over again following the club of operations.
To evaluate an algebraic expression means to notice the value of the expression when the variable is replaced by a given number. To evaluate an expression, nosotros substitute the given number for the variable in the expression and then simplify the expression using the guild of operations.
Example \(\PageIndex{1}\): evaluate
Evaluate \(x + vii\) when
- \(10 = 3\)
- \(x = 12\)
Solution
- To evaluate, substitute \(3\) for \(x\) in the expression, so simplify.
| \(x + 7\) | |
| Substitute. | \(\textcolor{carmine}{3} + 7\) |
| Add. | \(10\) |
When \(10 = 3\), the expression \(10 + 7\) has a value of \(10\).
- To evaluate, substitute \(12\) for \(x\) in the expression, so simplify.
| \(10 + 7\) | |
| Substitute. | \(\textcolor{red}{12} + seven\) |
| Add together. | \(nineteen\) |
When \(10 = 12\), the expression \(x + vii\) has a value of \(xix\). Notice that we got different results for parts (a) and (b) fifty-fifty though we started with the same expression. This is because the values used for \(x\) were different. When we evaluate an expression, the value varies depending on the value used for the variable.
exercise \(\PageIndex{ane}\)
Evaluate: \(y + 4\) when
- \(y = 6\)
- \(y = 15\)
- Answer a
-
\(ten\)
- Answer b
-
\(nineteen\)
exercise \(\PageIndex{ii}\)
Evaluate: \(a − v\) when
- \(a = 9\)
- \(a = 17\)
- Answer a
-
\(4\)
- Respond b
-
\(12\)
Example \(\PageIndex{2}\)
Evaluate \(9x − 2\), when
- \(x = 5\)
- \(ten = 1\)
Solution
Remember \(ab\) means \(a\) times \(b\), and then \(9x\) means \(9\) times \(x\).
- To evaluate the expression when \(x = 5\), we substitute \(5\) for \(x\), and so simplify.
| \(9x - two\) | |
| Substitute \(\textcolor{red}{5}\) for ten. | \(nine \cdot \textcolor{cherry-red}{5} - 2\) |
| Multiply. | \(45 - 2\) |
| Subtract. | \(43\) |
- To evaluate the expression when \(x = one\), nosotros substitute \(1\) for \(x\), and and then simplify.
| \(9x - 2\) | |
| Substitute \(\textcolor{red}{i}\) for x. | \(nine \cdot \textcolor{cherry}{1} - 2\) |
| Multiply. | \(9 - ii\) |
| Subtract. | \(7\) |
Discover that in part (a) that we wrote \(9 • 5\) and in office (b) we wrote \(9(i)\). Both the dot and the parentheses tell us to multiply.
exercise \(\PageIndex{3}\)
Evaluate: \(8x − 3\), when
- \(x = 2\)
- \(x = 1\)
- Respond a
-
\(xiii\)
- Answer b
-
\(five\)
do \(\PageIndex{4}\)
Evaluate: \(4y − 4\), when
- \(y = 3\)
- \(y = 5\)
- Answer a
-
\(8\)
- Answer b
-
\(16\)
Case \(\PageIndex{3}\): evaluate
Evaluate \(ten^2\) when \(x = 10\).
Solution
We substitute \(10\) for \(ten\), and and so simplify the expression.
| \(x^{2}\) | |
| Substitute \(\textcolor{red}{10}\) for ten. | \(\textcolor{red}{10}^{2}\) |
| Utilize the definition of exponent. | \(10 \cdot x\) |
| Multiply | \(100\) |
When \(ten = x\), the expression \(x^ii\) has a value of \(100\).
exercise \(\PageIndex{v}\)
Evaluate: \(ten^2\) when \(10 = eight\).
- Reply
-
\(64\)
exercise \(\PageIndex{6}\)
Evaluate: \(x^3\) when \(x = 6\).
- Reply
-
\(216\)
Example \(\PageIndex{four}\): evaluate
Evaluate \(2^x\) when \(x = 5\).
Solution
In this expression, the variable is an exponent.
| \(ii^{x}\) | |
| Substitute \(\textcolor{ruby}{5}\) for x. | \(2^{\textcolor{red}{5}}\) |
| Utilise the definition of exponent. | \(two \cdot 2 \cdot 2 \cdot two \cdot ii\) |
| Multiply | \(32\) |
When \(x = five\), the expression \(2^10\) has a value of \(32\).
do \(\PageIndex{vii}\)
Evaluate: \(2^10\) when \(x = 6\).
- Answer
-
\(64\)
exercise \(\PageIndex{8}\)
Evaluate: \(3^x\) when \(x = 4\).
- Answer
-
\(81\)
Example \(\PageIndex{five}\): evaluate
Evaluate \(3x + 4y − 6\) when \(x = 10\) and \(y = two\).
Solution
This expression contains ii variables, so nosotros must make two substitutions.
| \(3x + 4y − half-dozen\) | |
| Substitute \(\textcolor{red}{x}\) for x and \(\textcolor{blue}{ii}\) for y. | \(3(\textcolor{ruby-red}{10}) + 4(\textcolor{blueish}{2}) − 6\) |
| Multiply. | \(30 + 8 - 6\) |
| Add together and subtract left to right. | \(32\) |
When \(x = 10\) and \(y = 2\), the expression \(3x + 4y − 6\) has a value of \(32\).
exercise \(\PageIndex{9}\)
Evaluate: \(2x + 5y − 4\) when \(10 = 11\) and \(y = 3\)
- Answer
-
\(33\)
exercise \(\PageIndex{10}\)
Evaluate: \(5x − 2y − 9\) when \(x = 7\) and \(y = 8\)
- Answer
-
\(10\)
Instance \(\PageIndex{half dozen}\): evaluate
Evaluate \(2x^2 + 3x + 8\) when \(x = 4\).
Solution
We need to exist careful when an expression has a variable with an exponent. In this expression, \(2x^ii\) means \(2 • x • ten\) and is different from the expression \((2x)^2\), which means \(2x • 2x\).
| \(2x^{two} + 3x + viii\) | |
| Substitute \(\textcolor{red}{4}\) for each 10. | \(ii(\textcolor{red}{4})^{2} + iii(\textcolor{red}{4}) + 8\) |
| Simplify 4ii. | \(2(16) + 3(four) + 8\) |
| Multiply. | \(32 + 12 + 8\) |
| Add. | \(52\) |
exercise \(\PageIndex{11}\)
Evaluate: \(3x^ii + 4x + 1\) when \(x = 3\).
- Reply
-
\(forty\)
exercise \(\PageIndex{12}\)
Evaluate: \(6x^ii − 4x − seven\) when \(x = 2\).
- Answer
-
\(9\)
Identify Terms, Coefficients, and Like Terms
Algebraic expressions are fabricated upward of terms. A term is a abiding or the product of a constant and one or more variables. Some examples of terms are \(7\), \(y\), \(5x^ii\), \(9a\), and \(13xy\).
The abiding that multiplies the variable(s) in a term is called the coefficient. We can recall of the coefficient as the number in forepart of the variable. The coefficient of the term \(3x\) is \(3\). When we write \(x\), the coefficient is \(1\), since \(x = one • x\). Tabular array \(\PageIndex{ane}\) gives the coefficients for each of the terms in the left column.
| Term | Coefficient |
|---|---|
| 7 | seven |
| 9a | ix |
| y | one |
| 5x2 | five |
An algebraic expression may consist of 1 or more terms added or subtracted. In this affiliate, we will only piece of work with terms that are added together. Table \(\PageIndex{2}\) gives some examples of algebraic expressions with various numbers of terms. Notice that nosotros include the operation before a term with it.
| Expression | Terms |
|---|---|
| 7 | vii |
| y | y |
| x + 7 | x, vii |
| 2x + 7y + 4 | 2x, 7y, 4 |
| 3x2 + 4xtwo + 5y + 3 | 3xtwo, 4x2, 5y, iii |
Example \(\PageIndex{7}\):
Identify each term in the expression \(9b + 15x^2 + a + 6\). And so identify the coefficient of each term.
Solution
The expression has four terms. They are \(9b\), \(15x^two\), \(a\), and \(6\).
The coefficient of \(9b\) is \(9\).
The coefficient of \(15x^ii\) is \(xv\).
Call back that if no number is written before a variable, the coefficient is \(ane\). And so the coefficient of a is \(ane\).
The coefficient of a constant is the constant, so the coefficient of \(6\) is \(6\).
practice \(\PageIndex{13}\)
Identify all terms in the given expression, and their coefficients: \(4x + 3b + 2\)
- Answer
-
The terms are \(4x, 3b,\) and \(2\). The coefficients are \(4, 3,\) and \(2\).
do \(\PageIndex{14}\)
Identify all terms in the given expression, and their coefficients: \(9a + 13a^2 + a^3\)
- Answer
-
The terms are \(9a, 13a^ii,\) and \(a^three\), The coefficients are \(9, 13,\) and \(1\).
Some terms share common traits. Await at the following terms. Which ones seem to accept traits in common?
\(5x, 7, n^{two}, 4, 3x, 9n^{2}\)
Which of these terms are like terms?
- The terms \(7\) and \(4\) are both abiding terms.
- The terms \(5x\) and \(3x\) are both terms with \(ten\).
- The terms \(n^two\) and \(9n^2\) both have \(n^2\).
Terms are chosen like terms if they take the same variables and exponents. All abiding terms are besides similar terms. So among the terms \(5x, 7, n^two, iv, 3x, 9n^ii, 7\) and \(iv\) are like terms, \(5x\) and \(3x\) are like terms, and \(n^2\) and \(9n^2\) are like terms.
Definition: Like terms
Terms that are either constants or have the same variables with the aforementioned exponents are like terms.
Example \(\PageIndex{viii}\): identify
Identify the like terms:
- \(y^3, 7x^ii, 14, 23, 4y^3, 9x, 5x^ii\)
- \(4x^ii + 2x + 5x^2 + 6x + 40x + 8xy\)
Solution
- \(y^3, 7x^2, fourteen, 23, 4y^3, 9x, 5x^2\)
Await at the variables and exponents. The expression contains \(y^3, x^ii, x\), and constants. The terms \(y^3\) and \(4y^iii\) are like terms because they both accept \(y^3\). The terms \(7x^two\) and \(5x^2\) are like terms considering they both have \(x^2\). The terms \(fourteen\) and \(23\) are like terms considering they are both constants. The term \(9x\) does not take any like terms in this list since no other terms have the variable \(x\) raised to the ability of \(1\).
- \(4x^2 + 2x + 5x^2 + 6x + 40x + 8xy\)
Look at the variables and exponents. The expression contains the terms \(4x^2, 2x, 5x^2, 6x, 40x\), and \(8xy\) The terms \(4x^ii\) and \(5x^2\) are like terms because they both have \(x^2\). The terms \(2x, 6x\), and \(40x\) are like terms because they all have \(x\). The term \(8xy\) has no like terms in the given expression because no other terms contain the two variables \(xy\).
exercise \(\PageIndex{15}\)
Place the similar terms in the listing or the expression: \(9, 2x^3, y^ii, 8x^3, 15, 9y, 11y^2\)
- Answer
-
\(ix, 15\); \(2x^3\) and \(8x^iii\), \(y^two\), and \(11y^ii\)
do \(\PageIndex{16}\)
Place the like terms in the list or the expression: \(4x^iii + 8x^2 + 19 + 3x^2 + 24 + 6x^3\)
- Answer
-
\(4x^iii\) and \(6x^3\); \(8x^2\) and \(3x^ii\); \(19\) and \(24\)
Simplify Expressions by Combining Like Terms
Nosotros tin can simplify an expression by combining the like terms. What do yous think \(3x + 6x\) would simplify to? If you thought \(9x\), you lot would be correct!
We tin see why this works by writing both terms as addition problems.
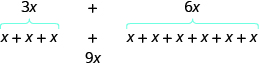
Add together the coefficients and keep the same variable. It doesn't matter what \(x\) is. If you have \(3\) of something and add \(6\) more of the same matter, the result is \(nine\) of them. For example, \(iii\) oranges plus \(6\) oranges is \(9\) oranges. We will discuss the mathematical properties backside this later.
The expression \(3x + 6x\) has just two terms. When an expression contains more terms, it may exist helpful to rearrange the terms and then that like terms are together. The Commutative Property of Addition says that nosotros can alter the order of addends without irresolute the sum. So we could rearrange the following expression earlier combining like terms.
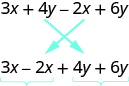
At present it is easier to see the like terms to be combined.
HOW TO: COMBINE LIKE TERMS
Step 1. Identify like terms.
Step 2. Rearrange the expression so like terms are together.
Footstep three. Add together the coefficients of the like terms.
Example \(\PageIndex{9}\): simplify
Simplify the expression: \(3x + 7 + 4x + 5\).
Solution
| \(3x + 7 + 4x + 5\) | |
| Identify the similar terms | \(\textcolor{ruddy}{3x} + \textcolor{bluish}{7} + \textcolor{cerise}{4x} + \textcolor{blue}{5}\) |
| Rearrange the expression, and then the like terms are together. | \(\textcolor{ruby-red}{3x} + \textcolor{red}{4x} + \textcolor{blue}{7} + \textcolor{blue}{5}\) |
| Add the coefficients of the like terms. | \(\textcolor{red}{7x} + \textcolor{bluish}{12}\) |
| The original expression is simplified to... | \(7x + 12\) |
practise \(\PageIndex{17}\)
Simplify: \(7x + 9 + 9x + 8\)
- Reply
-
\(16x+17\)
do \(\PageIndex{18}\)
Simplify: \(5y + 2 + 8y + 4y + 5\)
- Answer
-
\(17y+7\)
Example \(\PageIndex{10}\): simplify
Simplify the expression: \(7x^2 + 8x + ten^2 + 4x\).
Solution
| \(7x^{2} + 8x + x^{2} + 4x\) | |
| Identify the similar terms. | \(\textcolor{red}{7x^{two}} + \textcolor{blue}{8x} + \textcolor{reddish}{ten^{2}} + \textcolor{blue}{4x}\) |
| Rearrange the expression so like terms are together. | \(\textcolor{red}{7x^{2}} + \textcolor{red}{x^{2}} + \textcolor{bluish}{8x} + \textcolor{blue}{4x}\) |
| Add the coefficients of the like terms. | \(\textcolor{red}{8x^{two}} + \textcolor{blue}{12x}\) |
These are non like terms and cannot be combined. So \(8x^2 + 12x\) is in simplest form.
do \(\PageIndex{19}\)
Simplify: \(3x^2 + 9x + 10^ii + 5x\)
- Respond
-
\(4x^2+14x\)
practise \(\PageIndex{20}\)
Simplify: \(11y^2 + 8y + y^2 + 7y\)
- Answer
-
\(12y^two+15y\)
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.
Source: https://math.libretexts.org/Bookshelves/PreAlgebra/Book:_Prealgebra_%28OpenStax%29/02:_Introduction_to_the_Language_of_Algebra/2.03:_Evaluate_Simplify_and_Translate_Expressions_%28Part_1%29
0 Response to "Chapter 1 Test Review What Is the Value of the Expression (-8)^4"
Post a Comment